How To Find The Gcf With Exponents

Foundations

14 Greatest Common Cistron and Gene by Group

Learning Objectives

By the end of this section, y'all will exist able to:

Find the greatest common cistron of 2 or more expressions
Factor the greatest common cistron from a polynomial
Factor past grouping

Before you get started, take this readiness quiz.

Factor 56 into primes.
If you lot missed this problem, review (Effigy).
Find the least common multiple of 18 and 24.
If y'all missed this problem, review (Figure).
Simplify $-3\left(6a+11\right)$ .
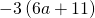If y'all missed this trouble, review (Figure).

Notice the Greatest Mutual Factor of Two or More Expressions

Earlier we multiplied factors together to become a product. Now, we will be reversing this procedure; nosotros will start with a product and then break information technology downwards into its factors. Splitting a product into factors is called factoring.

This figure has two factors being multiplied. They are 8 and 7. Beside this equation there are other factors multiplied. They are 2x and (x+3). The product is given as 2x^2 plus 6x. Above the figure is an arrow towards the right with multiply inside. Below the figure is an arrow to the left with factor inside.

We take learned how to factor numbers to find the least mutual multiple (LCM) of two or more numbers. Now nosotros will factor expressions and find the greatest mutual factor of 2 or more expressions. The method we utilise is similar to what we used to detect the LCM.

Greatest Common Factor

The greatest common factor (GCF) of 2 or more expressions is the largest expression that is a cistron of all the expressions.

First we'll detect the GCF of two numbers.

How to Discover the Greatest Common Gene of Two or More Expressions

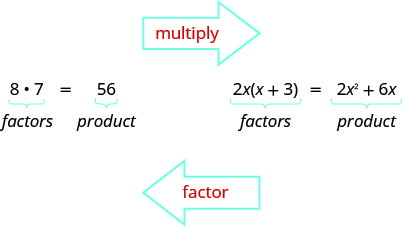
Observe the GCF of 54 and 36.

Solution

This table has three columns. In the first column are the steps for factoring. The first row has the first step, factor each coefficient into primes and write all variables with exponents in expanded form. The second column in the first row has The second row has the second step of The third row has the step The fourth row has the fourth step

Notice that, because the GCF is a factor of both numbers, 54 and 36 can exist written as multiples of 18.

$\begin{array}{c}54=18·3\hfill \\ 36=18·2\hfill \end{array}$

Observe the GCF of 48 and 80.

sixteen

Discover the GCF of 18 and 40.

We summarize the steps nosotros employ to detect the GCF below.

Discover the Greatest Common Gene (GCF) of two expressions.

Factor each coefficient into primes. Write all variables with exponents in expanded class.
List all factors—matching mutual factors in a cavalcade. In each column, circle the common factors.
Bring down the common factors that all expressions share.
Multiply the factors.

In the first example, the GCF was a constant. In the adjacent two examples, nosotros will go variables in the greatest common factor.

Find the greatest common factor of $27{x}^{3}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}18{x}^{4}$ .

Find the GCF: $12{x}^{2},18{x}^{3}$ .

$6{x}^{2}$

Find the GCF: $16{y}^{2},24{y}^{3}$ .

$8{y}^{2}$

Observe the GCF of $4{x}^{2}y,6x{y}^{3}$ .

Find the GCF: $6a{b}^{4},8{a}^{2}b$ .

$2ab$

Notice the GCF: $9{m}^{5}{n}^{2},12{m}^{3}n$ .

$3{m}^{3}n$

Find the GCF of: $21{x}^{3},9{x}^{2},15x$ .

Find the greatest common factor: $25{m}^{4},35{m}^{3},20{m}^{2}$ .

$5{m}^{2}$

Find the greatest mutual gene: $14{x}^{3},70{x}^{2},105x$ .

$7x$

Gene the Greatest Common Factor from a Polynomial

Just like in arithmetic, where it is sometimes useful to represent a number in factored form (for example, 12 as $2·6\phantom{\rule{0.2em}{0ex}}\text{or}\phantom{\rule{0.2em}{0ex}}3·4\right),$ in algebra, it can be useful to represent a polynomial in factored form. One way to exercise this is by finding the GCF of all the terms. Remember, nosotros multiply a polynomial by a monomial as follows:

$\begin{array}{cccc}\hfill 2\left(x+7\right)\hfill & & & \text{factors}\hfill \\ \hfill 2·x+2·7\hfill & & & \\ \hfill 2x+14\hfill & & & \text{product}\hfill \end{array}$

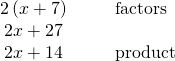
Now nosotros will get-go with a production, similar $2x+14$ , and stop with its factors, $2\left(x+7\right)$ . To do this nosotros use the Distributive Property "in reverse."

We country the Distributive Holding here simply as y'all saw it in earlier capacity and "in reverse."

Distributive Property

If $a,b,c$ are real numbers, then

$\begin{array}{ccccccc}a\left(b+c\right)=ab+ac\hfill & & & \text{and}\hfill & & & ab+ac=a\left(b+c\right)\hfill \end{array}$

The form on the left is used to multiply. The form on the right is used to factor.

So how exercise you utilize the Distributive Property to gene a polynomial? Y'all only find the GCF of all the terms and write the polynomial as a production!

How to Factor the Greatest Mutual Factor from a Polynomial

Factor: $4x+12$ .

Gene: $6a+24$ .

$6\left(a+4\right)$

Factor: $2b+14$ .

$2\left(b+7\right)$

Factor the greatest common factor from a polynomial.

Find the GCF of all the terms of the polynomial.
Rewrite each term every bit a product using the GCF.
Employ the "contrary" Distributive Property to factor the expression.
Check past multiplying the factors.

Factor equally a Substantive and a Verb

We use "factor" equally both a noun and a verb.

This figure has two statements. The first statement has

Cistron: $5a+5$ .

Factor: $14x+14$ .

$14\left(x+1\right)$

Factor: $12p+12$ .

$12\left(p+1\right)$

The expressions in the next example take several factors in mutual. Remember to write the GCF as the product of all the common factors.

Gene: $12x-60$ .

Gene: $18u-36$ .

$8\left(u-2\right)$

Factor: $30y-60$ .

$30\left(y-2\right)$

Now nosotros'll gene the greatest common factor from a trinomial. We start by finding the GCF of all three terms.

Gene: $4{y}^{2}+24y+28$ .

Factor: $5{x}^{2}-25x+15$ .

$5\left({x}^{2}-5x+3\right)$

Factor: $3{y}^{2}-12y+27$ .

$3\left({y}^{2}-4y+9\right)$

Gene: $5{x}^{3}-25{x}^{2}$ .

Cistron: $2{x}^{3}+12{x}^{2}$ .

$2{x}^{2}\left(x+6\right)$

Factor: $6{y}^{3}-15{y}^{2}$ .

$3{y}^{2}\left(2y-5\right)$

Factor: $21{x}^{3}-9{x}^{2}+15x$ .

Factor: $20{x}^{3}-10{x}^{2}+14x$ .

$2x\left(10{x}^{2}-5x+7\right)$

Gene: $24{y}^{3}-12{y}^{2}-20y$ .

$4y\left(6{y}^{2}-3y-5\right)$

Gene: $8{m}^{3}-12{m}^{2}n+20m{n}^{2}$ .

Factor: $9x{y}^{2}+6{x}^{2}{y}^{2}+21{y}^{3}$ .

$3{y}^{2}\left(3x+2{x}^{2}+7y\right)$

Gene: $3{p}^{3}-6{p}^{2}q+9p{q}^{3}$ .

$3p\left({p}^{2}-2pq+3{q}^{2}\right)$

When the leading coefficient is negative, we factor the negative out equally part of the GCF.

Factor: $-8y-24$ .

Factor: $-16z-64$ .

$-8\left(8z+8\right)$

Gene: $-9y-27$ .

$-9\left(y+3\right)$

Factor: $-6{a}^{2}+36a$ .

Cistron: $-4{b}^{2}+16b$ .

$-4b\left(b-4\right)$

Gene: $-7{a}^{2}+21a$ .

$-7a\left(a-3\right)$

Cistron: $5q\left(q+7\right)-6\left(q+7\right)$ .

Solution

The GCF is the binomial $q+7$ .


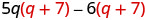Factor the GCF, (q + vii).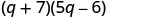
Cheque on your own by multiplying.

Cistron: $4m\left(m+3\right)-7\left(m+3\right)$ .

$\left(m+3\right)\left(4m-7\right)$

Factor: $8n\left(n-4\right)+5\left(n-4\right)$ .

$\left(n-4\right)\left(8n+5\right)$

Factor by Grouping

When at that place is no common factor of all the terms of a polynomial, await for a common factor in merely some of the terms. When there are four terms, a good way to start is past separating the polynomial into 2 parts with two terms in each part. Then look for the GCF in each part. If the polynomial can be factored, you will find a mutual cistron emerges from both parts.

(Non all polynomials can be factored. Just similar some numbers are prime, some polynomials are prime.)

How to Factor by Grouping

Cistron: $xy+3y+2x+6$ .

Gene: $xy+8y+3x+24$ .

$\left(x+8\right)\left(y+3\right)$

Factor: $ab+7b+8a+56$ .

$\left(a+7\right)\left(b+8\right)$

Factor by group.

Group terms with common factors.
Factor out the mutual factor in each group.
Factor the common factor from the expression.
Bank check by multiplying the factors.

Gene: ${x}^{2}+3x-2x-6$ .

Solution

$\begin{array}{cccc}\text{There is no GCF in all four terms.}\hfill & & & \hfill \phantom{\rule{4em}{0ex}}{x}^{2}+3x\phantom{\rule{0.5em}{0ex}}-2x-6\hfill \\ \text{Separate into two parts.}\hfill & & & \hfill \phantom{\rule{4em}{0ex}}\underset{⎵}{{x}^{2}+3x}\phantom{\rule{0.5em}{0ex}}\underset{⎵}{-2x-6}\hfill \\ \\ \\ \begin{array}{c}\text{Factor the GCF from both parts. Be careful}\hfill \\ \text{with the signs when factoring the GCF from}\hfill \\ \text{the last two terms.}\hfill \end{array}\hfill & & & \hfill \phantom{\rule{4em}{0ex}}\begin{array}{c}\hfill x\left(x+3\right)-2\left(x+3\right)\hfill \\ \hfill \left(x+3\right)\left(x-2\right)\hfill \end{array}\hfill \\ \\ \\ \text{Check on your own by multiplying.}\hfill & & & \end{array}$

Gene: ${x}^{2}+2x-5x-10$ .

$\left(x-5\right)\left(x+2\right)$

Cistron: ${y}^{2}+4y-7y-28$ .

$\left(y+4\right)\left(y-7\right)$

Key Concepts

Finding the Greatest Common Cistron (GCF): To find the GCF of ii expressions:
1. Factor each coefficient into primes. Write all variables with exponents in expanded form.
2. List all factors—matching mutual factors in a column. In each column, circumvolve the common factors.
3. Bring down the common factors that all expressions share.
4. Multiply the factors as in (Effigy).
Factor the Greatest Mutual Factor from a Polynomial: To factor a greatest common gene from a polynomial:
1. Notice the GCF of all the terms of the polynomial.
2. Rewrite each term as a product using the GCF.
3. Utilise the 'reverse' Distributive Property to gene the expression.
4. Check by multiplying the factors as in (Figure).
Factor by Grouping: To factor a polynomial with four four or more terms
1. Grouping terms with common factors.
2. Cistron out the common factor in each group.
3. Factor the common factor from the expression.
4. Bank check past multiplying the factors every bit in (Figure).

Practice Makes Perfect

Notice the Greatest Mutual Factor of Two or More Expressions

In the following exercises, find the greatest common gene.

$3x,10{x}^{2}$

$x$

$21{b}^{2},14b$

$8{w}^{2},24{w}^{3}$

$8{w}^{2}$

$30{x}^{2},18{x}^{3}$

$10{p}^{3}q,12p{q}^{2}$

$2pq$

$8{a}^{2}{b}^{3},10a{b}^{2}$

$12{m}^{2}{n}^{3},30{m}^{5}{n}^{3}$

$6{m}^{2}{n}^{3}$

$28{x}^{2}{y}^{4},42{x}^{4}{y}^{4}$

$10{a}^{3},12{a}^{2},14a$

$2a$

$20{y}^{3},28{y}^{2},40y$

$35{x}^{3},10{x}^{4},5{x}^{5}$

$5{x}^{3}$

$27{p}^{2},45{p}^{3},9{p}^{4}$

Factor the Greatest Common Cistron from a Polynomial

In the following exercises, factor the greatest common factor from each polynomial.

$4x+20$

$4\left(x+5\right)$

$8y+16$

$6m+9$

$3\left(2m+3\right)$

$14p+35$

$9q+9$

$9\left(q+1\right)$

$7r+7$

$8m-8$

$8\left(m-1\right)$

$4n-4$

$9n-63$

$9\left(n-7\right)$

$45b-18$

$3{x}^{2}+6x-9$

$3\left({x}^{2}+2x-3\right)$

$4{y}^{2}+8y-4$

$8{p}^{2}+4p+2$

$2\left(4{p}^{2}+2p+1\right)$

$10{q}^{2}+14q+20$

$8{y}^{3}+16{y}^{2}$

$8{y}^{2}\left(y+2\right)$

$12{x}^{3}-10x$

$5{x}^{3}-15{x}^{2}+20x$

$5x\left({x}^{2}-3x+4\right)$

$8{m}^{2}-40m+16$

$12x{y}^{2}+18{x}^{2}{y}^{2}-30{y}^{3}$

$6{y}^{2}\left(2x+3{x}^{2}-5y\right)$

$21p{q}^{2}+35{p}^{2}{q}^{2}-28{q}^{3}$

$-2x-4$

$-2\left(x+2\right)$

$-3b+12$

$5x\left(x+1\right)+3\left(x+1\right)$

$\left(x+1\right)\left(5x+3\right)$

$2x\left(x-1\right)+9\left(x-1\right)$

$3b\left(b-2\right)-13\left(b-2\right)$

$\left(b-2\right)\left(3b-13\right)$

$6m\left(m-5\right)-7\left(m-5\right)$

Factor by Group

In the post-obit exercises, factor past grouping.

$xy+2y+3x+6$

$\left(y+3\right)\left(x+2\right)$

$mn+4n+6m+24$

$uv-9u+2v-18$

$\left(u+2\right)\left(v-9\right)$

$pq-10p+8q-80$

${b}^{2}+5b-4b-20$

$\left(b-4\right)\left(b+5\right)$

${m}^{2}+6m-12m-72$

${p}^{2}+4p-9p-36$

$\left(p-9\right)\left(p+4\right)$

${x}^{2}+5x-3x-15$

Mixed Practise

In the following exercises, factor.

$-20x-10$

$-10\left(2x+1\right)$

$5{x}^{3}-{x}^{2}+x$

$3{x}^{3}-7{x}^{2}+6x-14$

$\left({x}^{2}+2\right)\left(3x-7\right)$

${x}^{3}+{x}^{2}-x-1$

${x}^{2}+xy+5x+5y$

$\left(x+y\right)\left(x+5\right)$

$5{x}^{3}-3{x}^{2}-5x-3$

Everyday Math

Area of a rectangle The area of a rectangle with length 6 less than the width is given by the expression ${w}^{2}-6w$ , where $w=$ width. Cistron the greatest common factor from the polynomial.

$w\left(w-6\right)$

Height of a baseball The height of a baseball game t seconds after it is hit is given by the expression $-16{t}^{2}+80t+4$ . Factor the greatest common factor from the polynomial.

Writing Exercises

The greatest common cistron of 36 and 60 is 12. Explain what this means.

Answers volition vary.

What is the GCF of ${y}^{4},{y}^{5},\text{and}\phantom{\rule{0.2em}{0ex}}{y}^{10}$ ? Write a general rule that tells you how to find the GCF of ${y}^{a},{y}^{b},\text{and}{y}^{c}$ .

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

This table has the following statements all to be preceded by

ⓑ If most of your checks were:

…confidently. Congratulations! Y'all take achieved your goals in this section! Reverberate on the report skills you used then that yous can go along to use them. What did you do to become confident of your ability to do these things? Be specific!

…with some help. This must be addressed quickly every bit topics you do non master get potholes in your road to success. Math is sequential—every topic builds upon previous work. Information technology is of import to make sure you have a strong foundation before yous motion on. Who can you ask for aid? Your fellow classmates and instructor are good resources. Is there a identify on campus where math tutors are bachelor? Can your study skills be improved?

…no – I don't get it! This is critical and you must not ignore it. You need to get assist immediately or you will speedily be overwhelmed. See your teacher as presently as possible to discuss your situation. Together yous can come up with a plan to get you lot the help you need.

Glossary

factoring: Factoring is splitting a product into factors; in other words, information technology is the reverse procedure of multiplying.

greatest common factor: The greatest mutual factor is the largest expression that is a factor of two or more than expressions is the greatest common factor (GCF).